Why Multiple Representations Matter….
Over the years, I’ve learned that children thrive when math is something they can touch, see, talk about, and eventually represent abstractly. Whether I’m supporting a hesitant learner or extending a confident one, my goal is always to help them build deep, lasting understanding and not just memorise steps.
Why Some Students Struggle
Many students develop math anxiety because they are introduced to symbols and procedures before they’ve made sense of the ideas behind them. Without a strong conceptual foundation, children rely on memorisation, leading to shaky confidence and frequent errors.
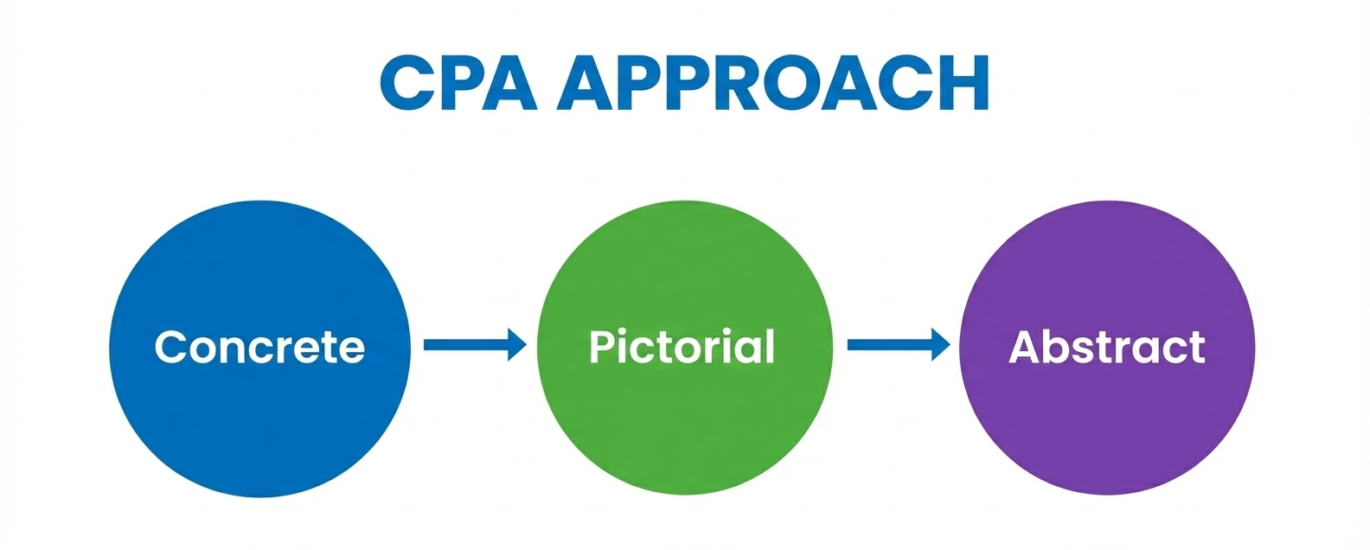
To prevent this, students need opportunities to explore concepts in multiple ways through hands-on tools, visuals, discussion, and real-life contexts. This is why the Concrete–Pictorial–Abstract (CPA) approach is central to my teaching.
How I Use the CPA Approach in My Sessions
1. Concrete: Building Meaning Through Hands-On Exploration
We begin with manipulatives such as counters, cubes, rekenreks, base-ten blocks, and fraction tiles. These tools help students experience the math before seeing any symbols. Concrete work reduces pressure and encourages curiosity. Students can build, test, adjust, and rebuild their ideas with confidence. Digital tools and virtual manipulatives can extend this hands-on exploration. Virtual base 10 blocks, fraction apps, interactive number lines and 3D shapes allow students to experiment with the concept in a dynamic way and visualise ideas digitally.
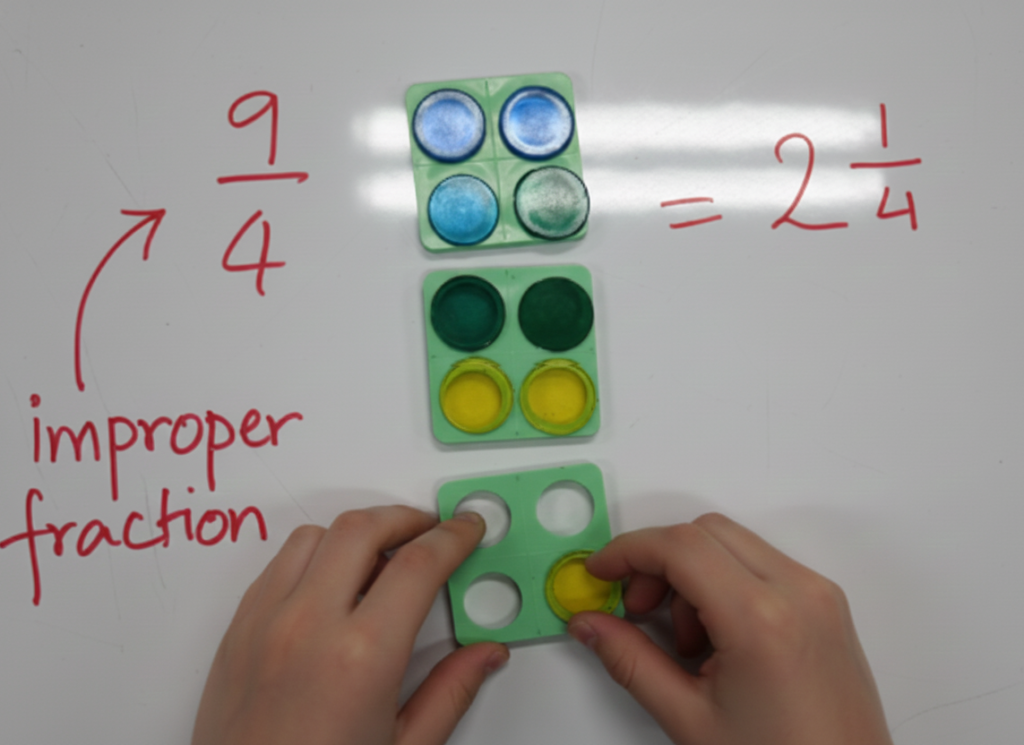
2. Pictorial: Making Thinking Visible
Once understanding grows, students represent their ideas using pictures and visual models such as number lines, bar models, arrays, area models, and simple sketches. This step helps students organise their thinking, recognise structure, and make connections between models and vocabulary. For many learners, this is the stage where concepts truly “click.”
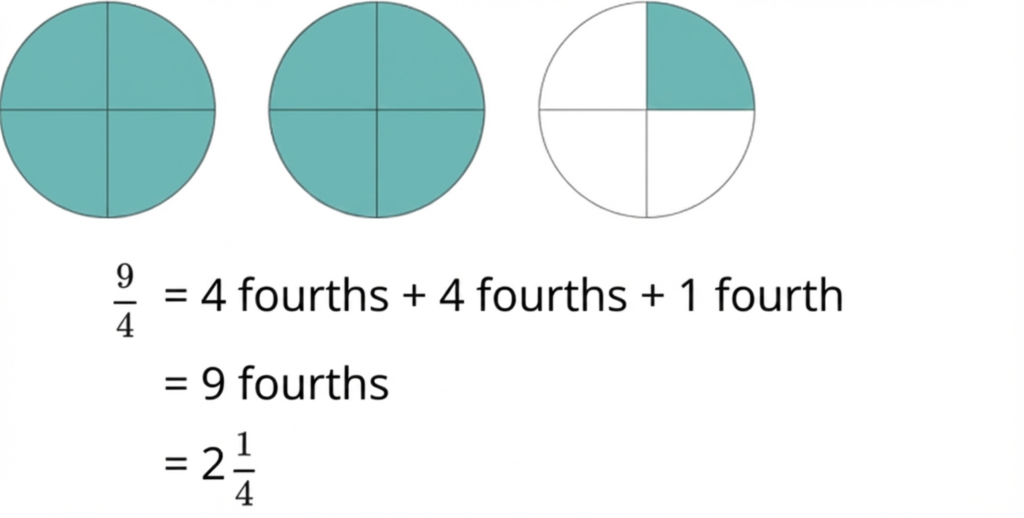
3. Abstract: Working Confidently with Symbols
When students are ready, we move to equations and notation. By this point, the abstract feels logical because it’s connected to experience and imagery. Students no longer guess or memorise. They understand what the symbols represent and why procedures work.
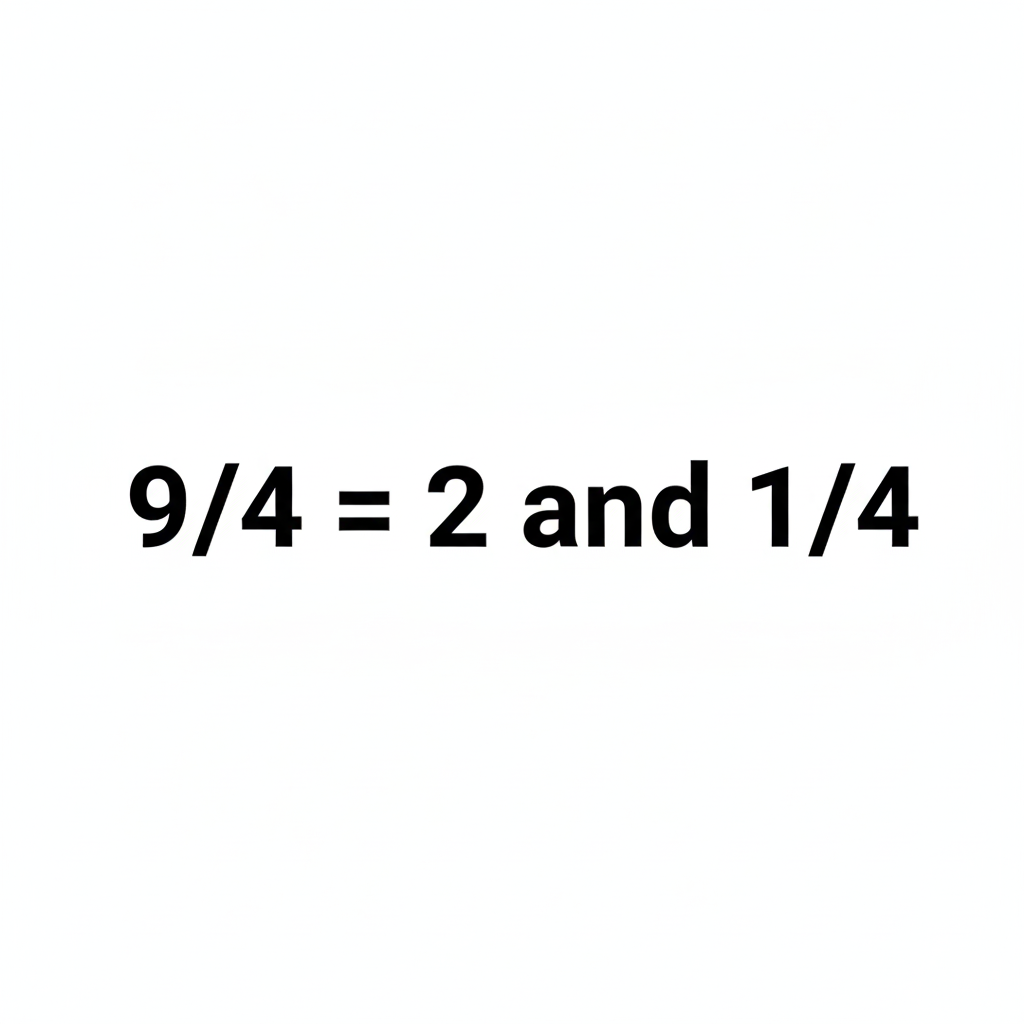
Strengthening Understanding with the Lesh Translation Model
The Lesh Translation Model further enriches learning by emphasizing five modes of representation:
- Concrete (manipulatives)
- Pictorial (visual models)
- Abstract (equations and notation)
- Contextual (real-world situations)
- Verbal (spoken or written reasoning)

A key part of my sessions is helping students move between these modes in meaningful ways. For example, students might first build or draw a model, then discuss their thinking with a partner, and finally write their own story problems to match the visuals. By creating context, explaining their reasoning, and representing ideas in multiple forms, students deepen their understanding and learn to apply concepts flexibly in new situations.
A Pathway to Confident, Joyful Mathematicians
When children learn through concrete tools, visuals, language, symbols, and meaningful contexts, they develop strong number sense and genuine mathematical confidence. They take risks, explain their thinking, and begin to see themselves as capable, curious mathematicians.
This thoughtful blend of the CPA approach and the Lesh Translation Model is at the heart of my practice guiding students from confusion to clarity and helping them build a joyful, lasting relationship with mathematics.
“When students can talk about math, draw it, see it, and model it—they truly understand it.”